
単純梁における曲げモーメントがかかった場合の応力計算方法について紹介します。
(誤りを含んでいましたらご指摘いただけると幸いです。)
今回は、H型鋼(H100x100x6x8)の先端に3000[N]の荷重をかけた場合に生じる応力値を求めることとします。
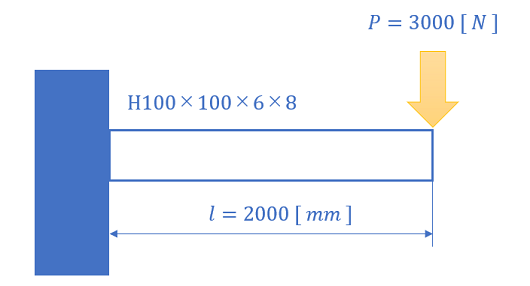
荷重 P 3000 [N]
梁の長さ l 2000 [mm]
断面係数 Z 76500 [mm3]
※本記事を参考にして計算する場合は自己責任にてお願いします。本記事によってトラブルが生じた場合にも一切責任は負いかねます。
応力値の計算方法
断面係数と曲げモーメントから応力値を求めるには以下の式を使います。
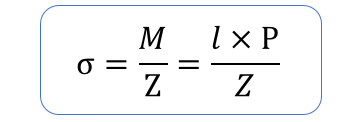
必要なパラメータの情報を計算しながら求めていきましょう。
断面係数とは
今回は与えられた条件の中に断面係数があるので、特に計算して求める必要はないのですがメモ書き程度に説明しておきます。
断面係数は、断面2次モーメントを中立軸からの距離で割った値です。
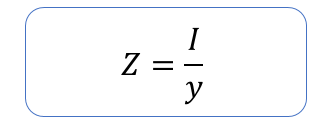
例えば、単純な長方形の断面を持つ梁の場合、 I=bh3/12 なので以下の式で表せます。
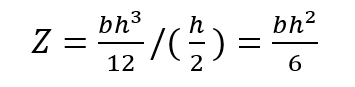
幅よりも高さに乗数がかかっているので、感覚的にも経験的にも縦に長い方が剛性が高いことが理解できると思います。
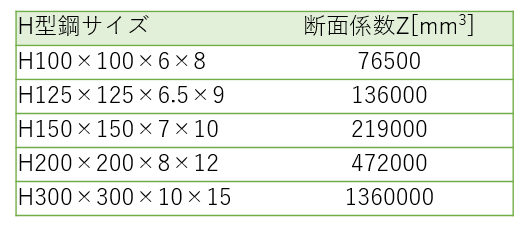
H型鋼の断面係数表
ご参考用にH形鋼の断面係数の表を載せておきます。
応力値の計算例
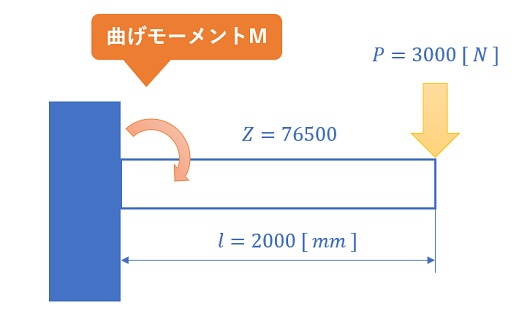
お待たせしました計算例を示します。
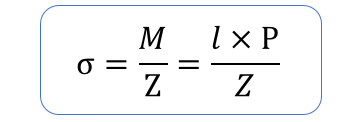
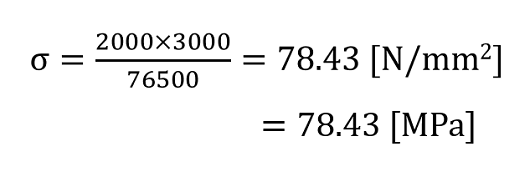
長さ2000[mm]のH型鋼(100x100x6x8)に3000[N]の荷重をかけると78.43[MPa]の応力が生じることが計算できました。
まとめ
断面係数がわかっていれば簡単に曲げ応力を求めることができることがわかりました。
しかしながら、実際の現場では補強のリブを入れるなど単純にH型鋼の断面係数だけで計算する機会は案外少ないかもしれませんね。
CADツールを使いながら断面二次モーメントを算出して計算している会社もあるでしょうし、解析ツールを使って強度解析している会社も多いと思います。
手計算の機会は減っているとは思いますが、計算式を頭に入れておくと形状をデザインする際にポイントをおさえられるので最適な解にたどりつきやすくなります。
以上、曲げ応力の計算方法についてのメモでした。
ご参考にしていただけると幸いです。





コメント