曲げ剛性について考える機会があったのでメモとして残します。
ついでに断面二次モーメントの参考値を載せました。
今回は、もやもやしながら記事を書いているのでもし間違いなどに気づきましたらご報告いただけると幸いです。
※本記事を参考にして計算する場合は自己責任にてお願いします。本記事によってトラブルが生じた場合にも一切責任は負いかねます。
断面二次モーメントとは
断面二次モーメントは、「部材の断面形状がもつ固さ」というイメージでしょうか。
感覚的に部材の形状によって固い方向があるのは想像できると思います。
例えば、垂直下向きの荷重に対して、板を横向きにした場合と縦向きの場合でどちらが強いでしょうか。
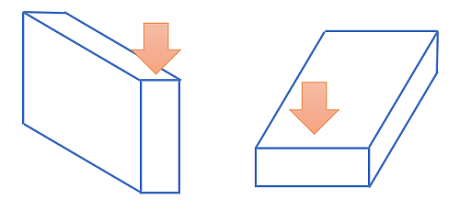
この強さを数値化したものが断面二次モーメントです。
(この記事では細かな理論は割愛します。)
長方形梁の断面二次モーメント
長方形梁の断面二次モーメントは以下の式で表せます。
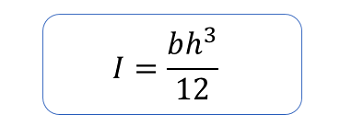
幅30mm、高さ50mmであれば、
![]()
高さに3乗がかかってるので、縦の長さが固さに影響が大きいということがわかります。
H形鋼の断面二次モーメント
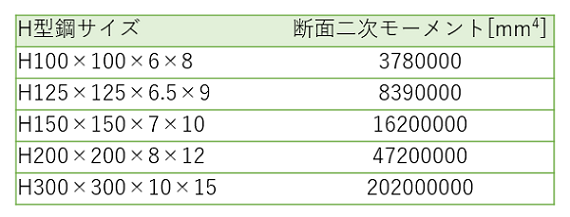
H型鋼の断面係数については下記の記事を参照ください。
断面係数から応力値を求める計算例を載せています。
パイプの断面二次モーメント
パイプの断面二次モーメントは以下の式で表せます。
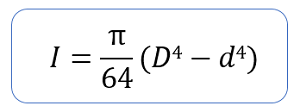
例えば、外径114.3mm、厚さ4.5mmの100A SGP管であれば、
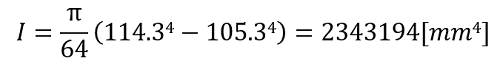
尚、断面係数は以下の式です。

参考に各サイズにおける断面二次モーメントを少し載せておきます。

曲げ剛性とは
曲げ剛性はその名前のとおり、曲げにくさを表します。
下の式でいうところの、EIが曲げにくさを表しています。
つまり、EIが曲げ剛性と考えてよさそうです。
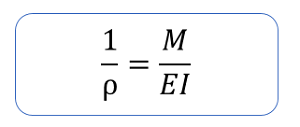
ρ:曲率半径
M:曲げモーメント
E:ヤング率
なぜEIが曲げにくさを表していると言えるのか
上の式におけるρは曲率半径を表しています。
曲率半径は曲がりが急であるほど小さく、緩やかであるほど大きくなります。
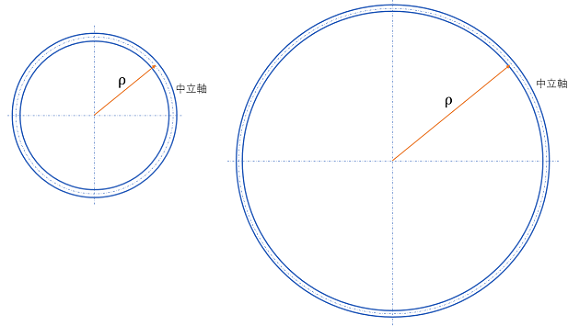
つまり、
半径が小さいほど曲がっている=曲がりやすい
半径が大きいほど曲げが緩やか=曲がりにくい
と考えればイメージしやすいかと思います。
式においてもρとEIは比例関係にあり、曲率半径が大きいほど曲げ剛性が大きいという関係になりそうです。
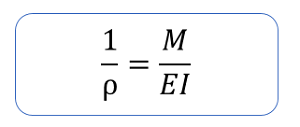
つまり、ここまで紹介してきた断面二次モーメントと材料の持つヤング率(縦弾性係数)の積が曲げ剛性です。
剛性が大きいほど変形しにくいというイメージとも一致します。
(部材の持つ形状と材質の持つ強さで、固さが決まることを示しています。)
まとめ
今回は断面二次モーメントや剛性の概念・イメージについて紹介しました。
断面二次モーメントを求める理論については触れてはいませんが、実際の実務でも断面二次モーメントを計算して求めることは少ない気がします。
(CADや解析ツールが主流ですね。)
応力値を計算する際の参考程度になっていれば幸いです。
(もちろんばりばりと手計算ででも断面二次モーメントを算出できるくらいになるに越したことはありません。)





コメント