
乱れがなく整然とした流れのことを層流、渦を伴って複雑に混じりあった流れを乱流と呼びます。
経験的には、蛇口から出る水によりイメージを掴めるかと思います。
はじめのうちは滑らかにガラス棒のように透き通っている状態(層流)から、蛇口を開けていくのに伴い流速が上がり、やがて水は乱れて流れ出ます(乱流)。
このように流れ方によって、圧力損失の計算への影響が大きいことが分かるかと思います。
今回はレイノルズ数の計算例を示して層流、乱流の判別の仕方を紹介します。
また、併せてダルシ―ワイズバッハ式による圧力損失の算出方法まで記載しておりますので参考にしてみてください。
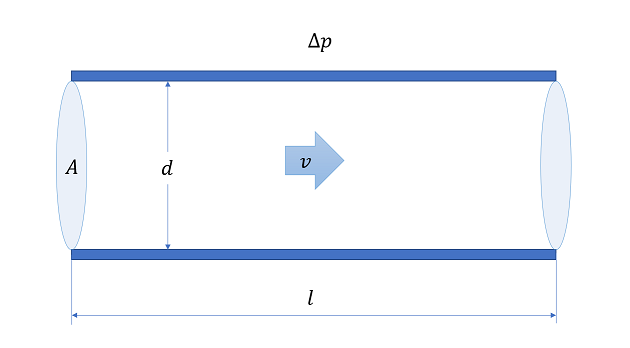
配管長さ 10 m
配管径 0.5 m
流量 300 L/min
動粘度 20×10-6 m2/s
油の密度 890kg/m3
※本記事を参考にして計算する場合は自己責任にてお願いします。本記事によってトラブルが生じた場合にも一切責任は負いかねます。
レイノルズ数の算出方法
まずは、連続の式から平均流速を求める
連続の式から流速を求めます。

ここで、与えられている流量Qの単位が[L/min]であることに注意します。
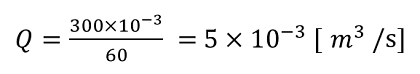
上式で単位を[m3/s]に合わせました。
始めの連続の式に戻り、流速を計算します。
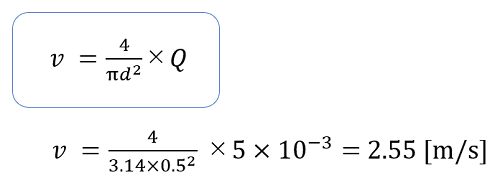
流速vが 2.55 [m/s]と求まりました。
レイノルズ数から層流か乱流か確認する
レイノルズ数は以下の式で計算します。
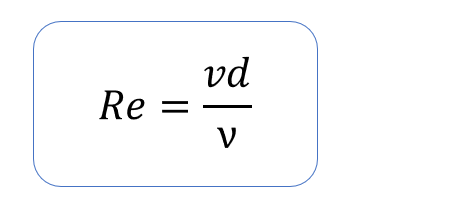
ここで、与えられている条件は以下のとおりでした。
配管長さ 10 m
配管径 0.5 m
動粘度 20×10-6 m2/s
油の密度 890kg/m3
レイノルズ数を計算すると以下のようになります。
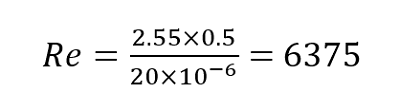
レイノルズ数は、Re > 2320 で乱流となるため、計算結果によると乱流であることがわかりました。
おまけ 管内圧力損失の計算方法
ブラジウスの式
ブラジウスの式より、レイノルズ数が以下の範囲である場合、
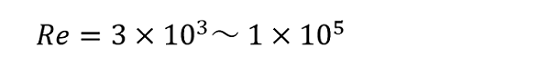
管摩擦係数は次式で求めることができます。
(これ以上のレイノルズ数の場合はニクラゼの式を使用ください。)
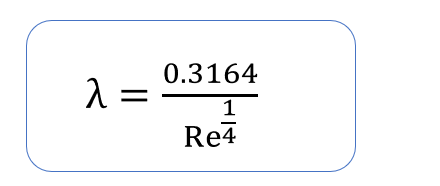
これを解くと、λ=0.0354 が得られます。
この式は管路内が滑らかな内壁での流れの実測値と一致することが確認されています。
ここで覚えておきたいのは、管摩擦係数λはレイノルズ数Reだけの関数では表現できず、管内の壁面粗さにも依存するということです。
つまり、最終的には壁面の相対粗さを考慮した計算を行う必要があります。
今回は壁面粗さについては説明を割愛していますが、壁面粗さについてんも計算例を参照したい方は下記の記事にて計算例をまとめていますので参照ください。
管摩擦係数まで求まったので管内圧損を計算
前項で求めた管摩擦係数から圧損を計算します。
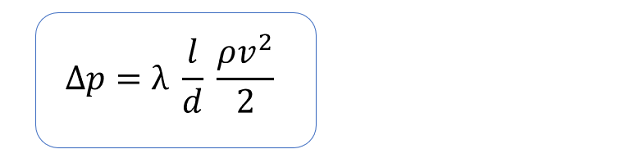
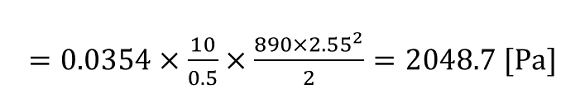
滑らかな内壁の場合、2048.7 [Pa]と求めることができました。
まとめ
今回は、油が流れる直径0.5mで長さ10mの配管の圧力損失について求めてみました。
尚、今回使用した油の動粘度はおよそ60℃程度の油の動粘度をイメージしています。
(正確な値は調べて使ってみてくださいね。)
小さいながらも損失が生じていることがわかりました。
バルブやオリフィスに比べると圧力損失はかなり小さいものではありますが、配管長さが長い場合や流速が大きい場合などは影響が大きくなってくるので計算が必要です。
以上、配管の圧力損失を計算する際に参考にしていただけると幸いです。





コメント