ベルヌーイの定理による圧力降下の導き方を紹介します。
今回は、水平な管路を水が2[m/s]の速度で流れている場合、その管内径が1/3に縮小すると圧力がどれだけ降下するか、を求める方法です。
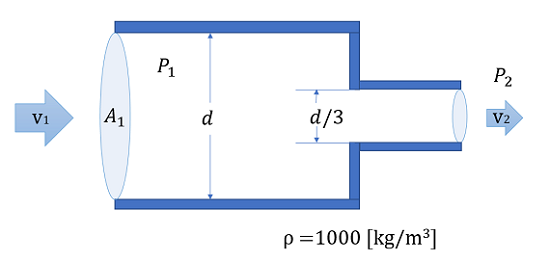
与えられている条件
入口流速 2 [m/s]
流体の密度 1000 [kg/m3]
入口径 d
出口径 d/3
入口流速 2 [m/s]
流体の密度 1000 [kg/m3]
入口径 d
出口径 d/3
※本記事を参考にして計算する場合は自己責任にてお願いします。本記事によってトラブルが生じた場合にも一切責任は負いかねます。
ベルヌーイの定理からP1-P2を導く
ベルヌーイの定理より、
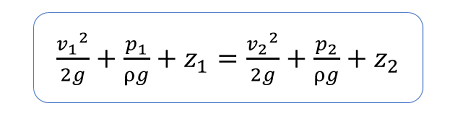
z1=z2として、
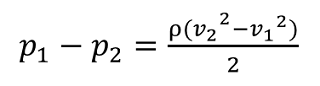
上記のようにP1-P2、即ち圧力降下のかたちにします。
連続の式から速度項をまとめる
連続の式から、v2について纏めます。
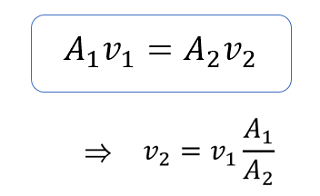
ベルヌーイの式と連続の式について解く
ベルヌーイの式と連続の式をまとめると、
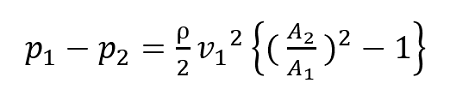
となります。
ここで、面積Aはそれぞれdで表すと、
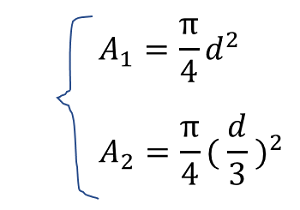
となるのでそれぞれ代入すると、
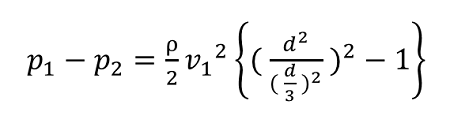
p1-p2についての式をv1, ρ, d で表すことができます。
数値を入れて計算する
与えられている条件をおさらいすると、

となり、数値を入れて計算すると、
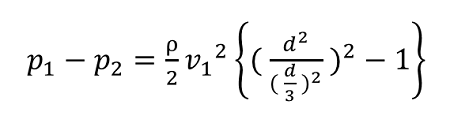
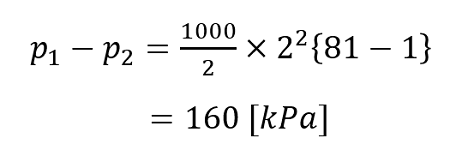
以上の式から、圧力降下は 160 [kPa] と求まりました。
まとめ
今回はベルヌーイの定理と連続の式による基本的な計算を行いました。
理論上では計算値はでるのですが、実際の圧力損失とはどれくらい整合がとれるのかはハテナです。
(流体は奥が深い。)
いつか実験的に圧力降下を求めて計算やCFDとの整合を取ってみたいと思っています。





コメント