
周方向の熱伸び量について計算する機会があったので、計算方法についてメモを残します。
熱伸びが拘束されている場合の応力は非常に大きな値となるので注意が必要です。
例えば、熱を受ける構造物を設計する際にはこの熱伸びを上手に逃がすor受けるように気を付ける必要があります。
今回は配管の熱伸びに対して構造物の健全性を見る機会があったので、配管の周方向の熱伸び量について計算をしています。
初期条件として与えられているのは、線膨張係数、温度差、配管の直径とします。
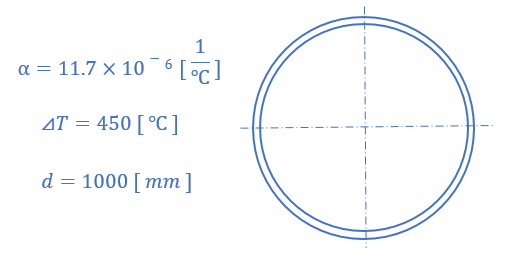
与えられている条件
線膨張係数 11.7×10-6 [1/℃]
温度差 450 [℃]
配管直径 1000 [mm]
線膨張係数 11.7×10-6 [1/℃]
温度差 450 [℃]
配管直径 1000 [mm]
※本記事を参考にして計算する場合は自己責任にてお願いします。本記事によってトラブルが生じた場合にも一切責任は負いかねます。
円周方向の熱伸び計算例
円周の熱伸び量を求める
円周の長さは、直径に円周率をかける。
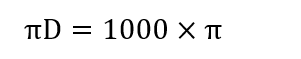
円周の長さは1000πとなります。
熱伸びの計算式より、円周の熱伸び量を計算します。
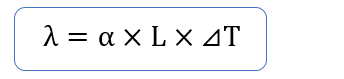
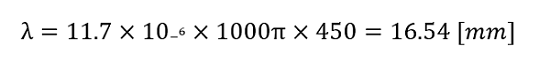
円周の長さは16.54mm伸びたことになります。
熱伸び後の直径D’
円周の伸び量がわかったので、この円周の長さから熱伸び後の直径を計算することができます。
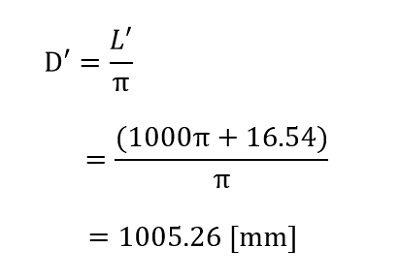
結果として、今回の条件においては直径方向に5.26mm伸びたことがわかりました。
まとめ
今回は拘束がない条件での熱伸び量を計算していることに注意してください。
拘束が加わる場合は伸び方(例えば、楕円状に広がる)なども変わるかと思います。
逆に特に拘束がかからない場合の周方向への熱伸び量は、今回のように周長さを計算する必要はなく、純粋に直径に線膨張係数と温度差かけると算出できるような気がします。(時間もないので理屈は追及しませんが。。)
以上、配管の周方向の熱伸び量計算方法についての計算メモでした。
ご参考にしていただけると幸いです。



コメント