タンク下配管からの流れについて計算する機会があったので、計算方法についてメモを残します。
今回は、流出流量、配管からの流出速度、圧力の損失について計算しています。
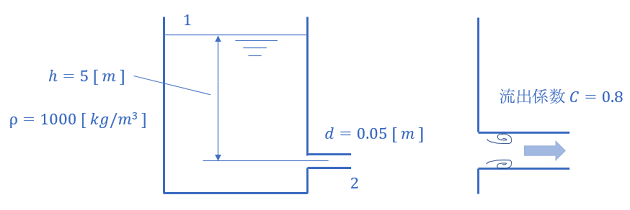
タンク下配管とタンク水面の高さ 5 m
タンク下配管径 0.05 m
流体の密度 1000 kg/m3
流出係数 0.8
※本記事を参考にして計算する場合は自己責任にてお願いします。本記事によってトラブルが生じた場合にも一切責任は負いかねます。
タンク流出流量、流速、圧力損失の計算方法(ベルヌーイの定理)
配管出口での流速はいくつか?
タンク水面と配管出口間に損失がないと仮定した場合、ベルヌーイの定理が成り立ちます。
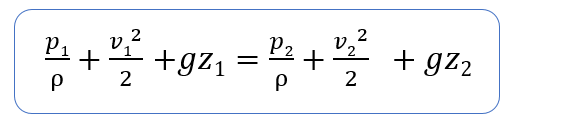
p1とp2は大気圧であり、p1=p2。
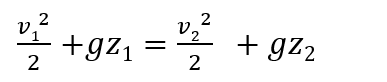
z1=h、z2=0なので、
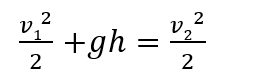
またタンク水面での速度はないので、v 1 =0。
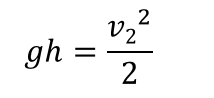
上式から配管出口での流速を求める。
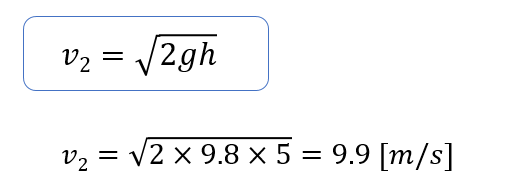
v2=9.9 [m/s]と求めることができました。
配管出口での流出流量はいくつか?
流量は連続の式より、
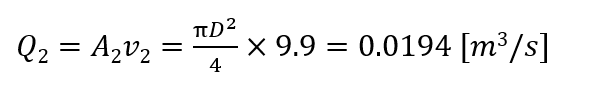
実際の流出流量は上記で得られた結果に流出係数Cをかけた値となるので、
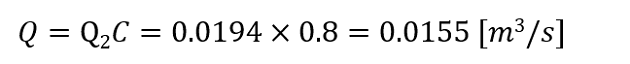
流出流量が0.0155[m3/s]と求まりました。
エネルギー損失はいくつか?
エネルギー損失があるとき、断面1と2の間で次のようなエネルギー保存則が成り立ちます。
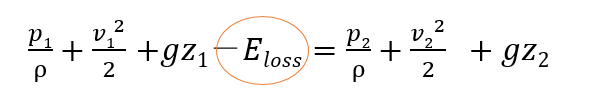
与えられている条件から、式を整理すると、
( p1=p2、 z 1 =h、z 2 =0、 v 1 =0)
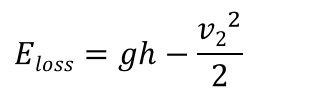
タンク配管出口での流速は流出流量Qと断面積A2から、
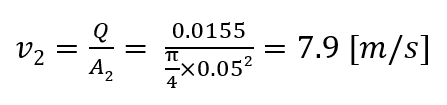
ここで求めたv2を エネルギー損失の式に代入して、
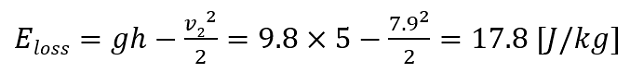
上記のようにエネルギー損失を求めることができました。
.
付録:単位換算(エネルギー損失→圧力損失)
エネルギー損失を圧力損失によって示します。
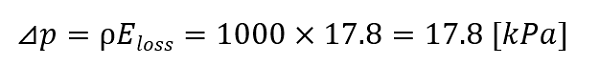
下記にはご参考用に計算上の単位を示しています。
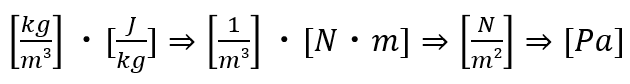
まとめ
ここまで紹介してきた計算式でタンク下配管からの流量、流速、圧力損失が計算できるかと思います。
今回は縮流係数は流出係数は初期条件として与えていますが、実際には実験値によって求めたデータ或いは大学や会社独自の参考値があるかもしれません。
私の手元には信頼に値するようなデータや数値はなかったので一般的に見かける数値を参照しました。(計算の仕方に焦点を当てているためです。)
以上、タンク下配管から流出する流体の計算方法についての計算メモでした。
ご参考にしていただけると幸いです。





コメント